Circuit

In ZK literature this usually refers to an arithmetic circuit: an ordered collection of additions and multiplications (and sometimes custom operations) that are applied to a set of inputs to yield an output.

The word “circuit” is used somewhat ambiguously, but most of the times we refer to an arithmetic circuit. An arithmetic circuit is an ordered collection of operations (e.g. addition, multiplication) represented by gates. These gates are connected by wires. Given an arithmetic circuit, we can apply an input signal, allow it to propagate through the wires and gates and observe the output. Below is an example of an arithmetic circuit that expects 3 inputs $x_0$, $x_1$ and $x_2$, and computes: $$y=5x_0+3(x_1+x_2)$$

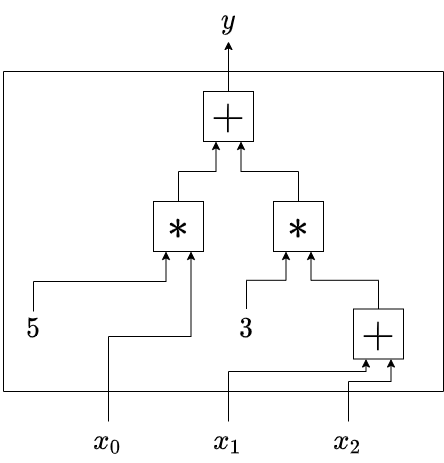
Why are we so obsessed with arithmetic circuits? Finding a set of input values that produce a desired output is a hard problem. This problem is known as the circuit satisfiability problem and has been heavily studied in complexity theory. One notable result is that any provable statement can be converted to the satisfiability problem (more formally, the circuit satisfiability problem is NP-complete). This comes in handy when we want to construct proof systems for generic statements.